A spherical shell of thermal conductivity k?has inside radius r₁ and outside radius r₂ (figure). The inside of the shell is held at a temperature T₁, and the outside at temperature T₂. In this problem, you are to show that the thermal current through the shell is given by Consider a spherical element of the shell of radius r?and thickness dr.

(a) Why must the thermal current through each such element be the same?

(b) Write the thermal current I?through such a shell element in terms of the area A = 4pr2, the thickness dr, and the temperature difference dT?across the element.

(c) Solve for dT?in terms of dr?and integrate from r?= r₁ to r?= r₂.

(d) Show that when r_1?and r₂ are much larger than r₂- r₁, Equation 21-22 is the same as Equation 21-7.

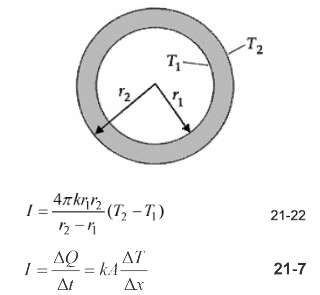
-T2 T,- knH (T, -) 21-22 . 21-7 = kA -