Managerial Accounting For Undergraduates 2nd Edition James Wallace, Scott Hobson, Theodore Christensen - Solutions
Discover the ultimate resource for mastering "Managerial Accounting For Undergraduates 2nd Edition" by James Wallace, Scott Hobson, and Theodore Christensen. Access comprehensive solutions and answers key to enhance your understanding. Whether you're seeking a solution manual, solutions PDF, or solved problems, our platform provides detailed step-by-step answers. Benefit from our extensive test bank, featuring chapter solutions and an instructor manual, tailored to meet your academic needs. Unlock the potential of your textbook with questions and answers readily available for free download, ensuring you excel in your studies.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


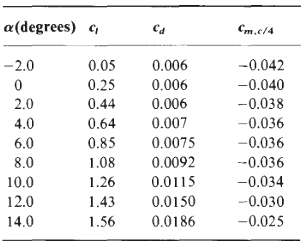
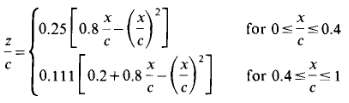
![|0.25| 0.8 for 0s-s0.4 х [02-03-()] 0.111 0.2+0.8 for 0.4<-s 1](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1552/4/6/8/9805c88cbf46e6771552512177100.jpg)