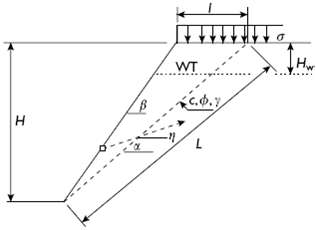
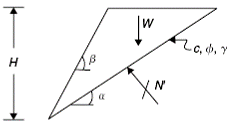
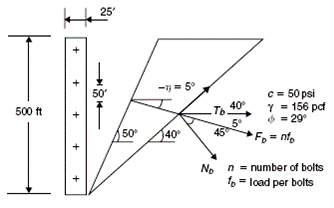
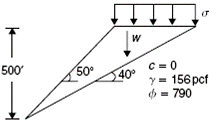
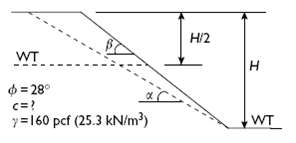
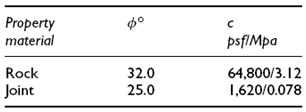
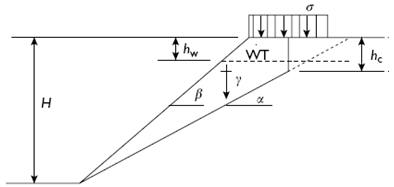
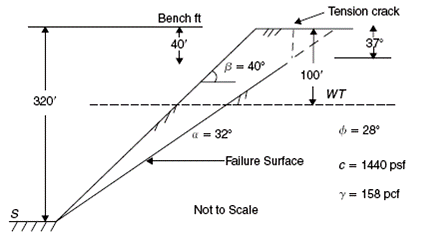
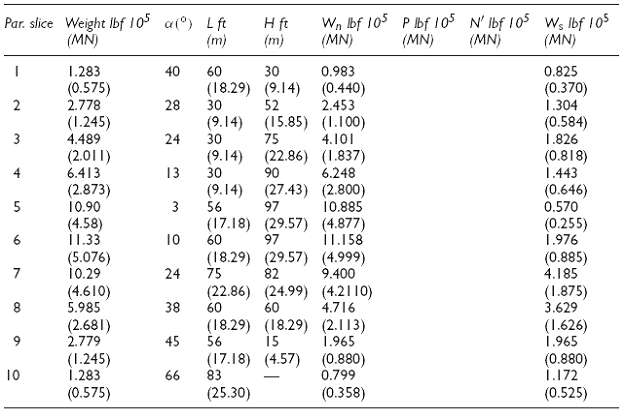
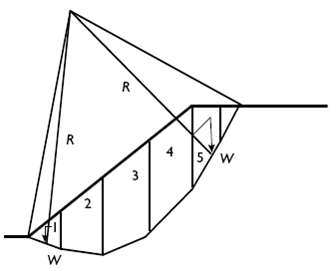
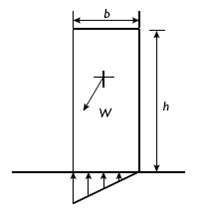
Design Analysis in Rock Mechanics 1st edition William G. Pariseau - Solutions

Unlock the potential of your studies with our comprehensive solutions for "Design Analysis in Rock Mechanics 1st edition" by William G. Pariseau. Access an extensive range of resources including an online answers key, solutions manual, and PDF solutions. Our collection features solved problems, test banks, and chapter solutions to enhance your understanding. Benefit from step-by-step answers and the instructor manual tailored to this textbook. Experience the convenience of free download options, ensuring you have the questions and answers you need at your fingertips for a seamless learning experience.