For m = 1,2,... and & integer, show that E(-1r () m 27) r=0

For m = 1,2,... and & integer, show that

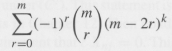
The proof is by induction. The result is easily checked for m = 1,2, 3. Then assume and show that

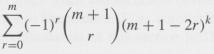
First, prove for k < m + 1. For this purpose, use the identity

And in the process of the subsequent parts of the proof, use the expansion

Along with. In establishing for k = m + 1, write (m + 1 - 2r)^m+l = (m + 1 - 2r)^m (m + 1 - 2r), use the fact that

Repeatedly use the expansion just mentioned, and, of course, also employs relation.

E(-1r (") m 27) r=0