For a function g = R C, set Îg (u) = g(u + h) - g(u - h),h R and define Î (n) g(u) recursively.

For a function g = R †’ C, set Δg (u) = g(u + h) - g(u - h),h ˆˆ R and define Δ⁽ⁿ⁾g(u) recursively. Then

(i) Show that   

(ii) From part (i), and by expanding f(t) around 0 up to terms of order 2n, obtain

(where o(t)/t †’ = as t †’ 0) so that

Part (i) is proved by induction in m. In the process of doing so, the relation

will be needed. In proving part (ii), the following relation is required (which you may use here without proof; see, however, the next exercise):

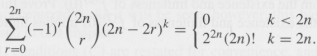
g(u) = E(-1y(" )e(u- (m) g(u + (m 2r)h). r=0