IfXandYare two identically distributed integrable r.v.s then

For any constant c.

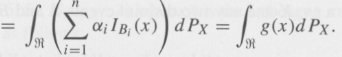
Now, let g be nonnegative. Then there exist 0 £ g_n(x) simple †‘ g(x); i.e.,

Which implies that 0 £

Simple †‘ g(X) as n†’¥ where A_ni = X^€“1(B_ni). Then

Whereas

For all n, by the previous step. Hence

Finally, for any g, write g(x) = g⁺ (x) €“ g^€“(x), which implies g(X) = g⁺(X) €“ g^€“ (X). Now, if f_Wg (X)d P exists, it then follows that either

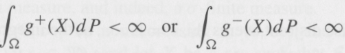
Or both. Since

And

By the pervious step, it follows that either

Or both, respectively, Thus, f_Âg(x)d Px exists and

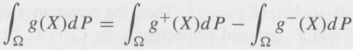
Likewise, the existence of f_Âg (x)d Px implies the existence of f_Wg (X)d P and their equality.

E [X1qX\s0] = E [Y IY\so)]