In this exercise we work with the Black-Scholes setting applied to foreign currency denominated assets. We will see a different use of Girsanov theorem. [for more detail see Musiela and Rutkowski (1997).] Let r,f denote the domestic and the foreign risk-free rates. Let S_t be the exchange rate, that is, the price of 1 unit of foreign currency in terms of domestic currency. Assume a geometric process for the dynamics of S_t;

dS_t = (r ? f)S_tdt + ?S_tdW_t.

(a) Show that where W_t is Wiener process under probability P.

(b) Is the process a martingale under measure P?

(c) Let P be the probability what does Girsonov theorem imply about the process, W_t ? ?_t,

?under P?

?(d) shown using Ito formula that

dZ_t = Z_t[(f ? r + ?²)dt ? ?dW_t]

where Z_t = 1/St.

(e) Under which probability is the process Z_te^rt f e^ft a martingale?

(f) Can we say that P is the arbitrage-free measure of the foreign economy?

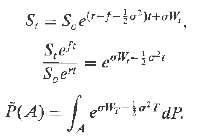
S, = S,er--lu+uW,. S,ef S,en = e,- P(A) = eo, jai dP.