![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


.png)
![-2] - 1 2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2023)-1.png)
-2.png)
.png)
-1.png)
-2.png)
-1.png)
![–1 6 3] 9_ 4 5 A = B = 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2030)-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
![Factory 3 4 Vehicle 30] SUV 100 90 40 20 A = 70 60] Pickup | Type 2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2038)-1.png)
![Resort Resort Resort Resort y х [615 670 740 995 1030 1180 1105] Quadruple 990] Double Оссирancy](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2038)-2.png)
![Outlet 2 1 125 100 75] Apples 100 175 125] Peaches 3 Crop](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2039)-1.png)
![Warehouse [5,000 4,000] A A = |6,000 10,000 B Model 8,000 5,000] c,](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2039)-2.png)
![Department Cutting Assembly Packaging 0.2 Small [1.0 S = |1.6 0.5 0.2 Medium Boat size 1.0 | 2.5 1.4] Large 2.0](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2040)-1.png)
![Factory B $15 $13] Cutting T = $12 $11 Assembly Department $11 $10] Packaging](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2040)-2.png)
-3.png)
![From 0.1 0.1] R [0.6 0.1 P = |0.2 0.7 0.1 D To 0.2 0.2 0.8 I](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2041).png)
![Calories burned 130-lb 155-lb person person [472 563] Basketball A = 590 704 | Jumping rope 177 211] Weight lifting](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2042).png)
![Factory B 25] Acoustic Г 70 35 35 100 50 Guitar type 70 Electric](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2048).png)
-1.png)
![10 5 -7] 4 3 2 -2](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2052)-2.png)
-3.png)
-1.png)
![1 -2] -3 2.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2053)-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-1.png)
-2.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
.png)
-1.png)
-2.png)
-3.png)
.png)
.png)
-1.png)
-2.png)
.png)
![b' A =: a d]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2069)-1.png)
-2.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
-1.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-3.png)
.png)
.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
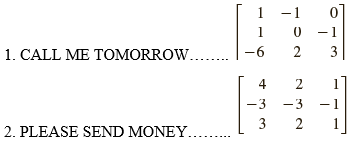
.png)
-1.png)
-2.png)
-1.png)
-2.png)
-1.png)
-2.png)
-3.png)
-1.png)
-1.png)
-2.png)
-3.png)
-1.png)
-2.png)
-1.png)
-2.png)
.png)
.png)
![31 1 1] 1 31 2 E으-으](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/image/images16/1383-M-C-P-E(2119).png)