Shape of free surface in tangential annular flow 

(a) A liquid is in the annular space between two vertical cylinders of radii KR and R, and the liquid is open to the atmosphere at the top. Show that when the inner cylinder rotates with an angular velocity Ω, and the outer cylinder is fixed, the free liquid surface has the shape in which zR is the height of the liquid at the outer-cylinder wall, and ζ = r/R. 

(b) Repeat (a) but with the inner cylinder fixed and the outer cylinder rotating with an angular velocity Ω_o. Show that the shape of the liquid surface is 

Draw a sketch comparing these two liquid-surface shapes.

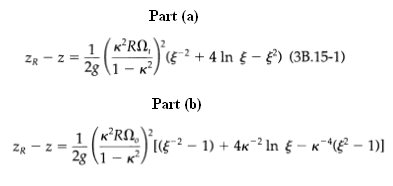
Part (a) 1 (K*RN, ZR - z 2g " |(5+ 4 In ) (3B.15-1) Part (b) 1(KRN,' 2g \1 - K (2 1) + 4K-2 In - K*( 1)]