Question: A stationary process X (t) is applied to a linear time-invariant filter of impulse response b (t), producing an output Y (t). (a) Show that

A stationary process X (t) is applied to a linear time-invariant filter of impulse response b (t), producing an output Y (t).

(a) Show that the cross-correlation function RYX (?) of the output Y (t) and the input X (t) is equal to the impulse response b (?) convolved with the autocorrelation function RX (?) of the input, as shown by, show that the second cross-correlation function RXY (?) equals

(b) Find the cross-spectral densities SYX (f) and SXY (f).

(c) Assuming that X (t) is a white noise process with zero mean and power spectral density N0/2, shows that. Comment on the practical significance of this result.

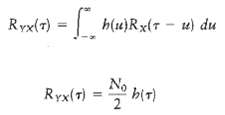
hlu)Rx(T - u) du Ryx(7) No Ryx(T) 2 bir)

Step by Step Solution

★★★★★

3.47 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a The crosscorrelation function Ryx T is Ryx T EYtT Xt The Yt and Xt are relat... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

19-E-T-E-C-S (11).docx

120 KBs Word File

Students Have Also Explored These Related Telecommunication Engineering Questions!

A torque T is applied to a thin-walled tube having a cross section in the shape of a regular hexagon with constant wall thickness t and side length b (see figure). Obtain formulas for the shear...

A 32-lb pull T is applied to a cord, which is wound securely around the inner hub of the drum. Determine the moment of T about the drum center C. At what angle q should T be applied so that the...

Let 0 v R3. (a) Show that the cross product Lv[x] = v x x defines a linear transformation on R3. (b) Find the 3 x 3 matrix representative Av of L, and show that it is skew-symmetric. (c) Show that...

networsksss [4 marks] (c) Write down a HOPLA term realising the parallel composition of PCCS. Use this to give an encoding of PCCS into HOPLA, specifying a HOPLA term JPK for every PCCS term P....

An ergodic real-valued random process $U(t)$ with autocorrelation function $\Gamma_{U}(\tau)=\left(N_{0} / 2 ight) \delta(\tau)$ is applied to the input of a linear, time-invariant filter with...

A zero-mean stationary process X (t) is applied to a linear filter whose impulse response is defined by a truncated exponential. Show that the power spectral density of the filter output y (t) is...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

MUST BE CORRECT ANSWERS A small software company has the following simplified cashflow, funded by shareholders' equity of 20,000 and a bank overdraft of 5000: Invoiced money received 2 months after...

1. Let X(t) denote a wide sense stationary process with X = 0 and autocorrelation RX(). Let Y(t) = 2 + X(t). What is RY(t,)? Is Y(t) wide sense stationary? 2. X(t), the input to a linear...

Problem 7 We will demonstrate the connection between the signal's expected spectrum and the signal's autocor- relation function through simulation of a discrete-time system. 1. Consider a filtered...

A uniform strut of mass m makes an angle 6 with the horizontal. It is supported by a frictionless pivot located at one-third its length from its lower left end and a horizontal rope at its upper...

You have seen that a double cone can be intersected with a plane to form a circle, an ellipse, a parabola, and a hyperbola. What shapes can be formed by the intersection of a plane and a square-based...

Effect of sample size on the sampling distribution. You are planning a study and are considering taking an SRS of either 200 or 400 observations. Explain how the sampling distribution would differ...

Refer to the data in Table P-18. Find the "best" regression model using the stepwise regression procedure and the all possible regressions procedure. Compare the results. Are you confident using a...

Sifting, the second department in a three-department production process for Finest Flour Inc., received 10,000 units with a total cost of $25,000 from Milling during May. Production costs in Sifting...

The scores for two within-term examinations, X1 and X2; the current grade point average (GPA), X3; and the final exam score, Y, for 20 students in a business statistics class are listed in Table...

For the year ended September 27, 2014, Apple, Inc., reported net income of $39,510 million. Total shareholders' equity on this date was $111,547 million, and on September 28, 2013, it was $123,549...

A zero coupon bond with a face value of $20,000 matures in 10 years. What should the bond be sold for now if its rate of return is to be 4.194% compounded annually? Refer to zero coupon bonds. A zero...

Name the compound Pb(C 2 H 3 O 2 ) 2 . a) Lead(II) carbonate b) Lead(II) acetate c) Lead bicarbonate d) Lead diacetate

When examining X-rays, radiologists often deal with four to six images at a time. For a faithful digital representation of an X-ray photograph, a pixel array of 2048 by 2048 is typically used with a...

Commonly, medical digital radiology ultrasound studies consist of about 25 images extracted from a full-motion ultrasound examination. Each image consists of 512 by 512 pixels, each with 8 bits of...

Identify the major types of equipment and communication redundancies found in today's data centers.

What are the differences among Tier 1, Tier 2, Tier 3, and Tier 4 data centers?

Why do businesses partner with third-party data centers?

You purchased a commercial office building for $2,200,000 one year ago. The appraisal noted the value of the land was worth $550,000. You financed the purchase through a debt instrument with a...