Illustrate Theorem 43.7, as we did in Example 43.8, for each of the following spaces. 

a. The annular region of Example 42.10 

b. The torus of Example 42.12 

c. The Klein bottle of Example 43.1

Data from Theorem 43.7

Let X be a finite simplicial complex (or triangulated space) of dimension ≤ Let χ(X) be the Euler characteristic of the space X, and let ,B_j be the Betti number of H_j(X). Then

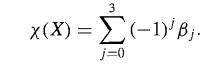
This theorem holds also for X of dimension greater than 3, with the obvious extension of the definition of the Euler characteristic to dimension greater than 3.

3 x(x) = (-1)/;. j=0