(a) When = n is a nonnegative integer, Hermites differential equation always possesses a polynomial solution of degree n. Use y 1 (x), given

(a) When α = n is a nonnegative integer, Hermite’s differential equation always possesses a polynomial solution of degree n. Use y₁(x), given in Problem 51, to find polynomial solutions for n = 0, n = 2, and n = 4.

Then use y₂(x) to find polynomial solutions for n = 1, n = 3, and n = 5.

(b) A Hermite polynomial H_n(x) is defined to be the nth degree polynomial solution of Hermite’s equation multiplied by an appropriate constant so that the coefficient of xⁿ in H_n(x) is 2_n. Use the polynomial solutions in part (a) to show that the first six Hermite polynomials are

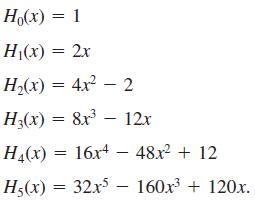
H(x) = 1 H(x) = 2x .() 4? 2 H3(x) = 8x 12x () 3D 164 48? + 12 () %3D 325 1603 + 120.