In Section 6.4 we saw that ty'' + y' + ty = 0 is Bessel’s equation of order n = 0. In view of (22) of that section and Table 6.4.1 a solution of the initial-value problem ty'' + y' + ty = 0, y(0) = 1, y'(0) = 0, is y = J₀(t). Use this result and the procedure outlined in the instructions to Problems 17 and 18 to show that

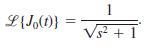
You might need to use Problem 46 in Exercises 7.2.

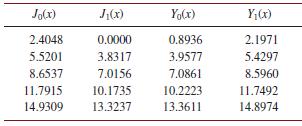
Table 6.4.1

Suppose f(t) is a function for which f'(t) is piecewise continuous and of exponential order c. Use results in this section and Section 7.1 to justify

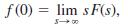
where F(s) = ℒ{ f(t)}. Verify this result with f(t) = cos kt.

1 %3D Vs? + 1