(a) Write a program for n × n matrices that prints every step. Apply it to the (nonsymmetric!) matrix (20 steps), starting from [1     1    1]^T.

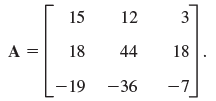
(b) Experiment in (a) with shifting. Which shift do you find optimal?

(c). Consider

and take

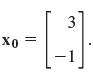
Show that for q = 0, δ = 1 all steps and the eigenvalues are ±1, so that the interval [q - δ, q + δ] cannot be shortened (by omitting ±1) without losing the inclusion property. Experiment with other x₀€™s.

(d) Find a (nonsymmetric) matrix for which δ in (2) is no longer an error bound.

15 12 3 A = 18 44 18 - 19 -36 -7 [0.6 0.8] A 0.8 -0.6