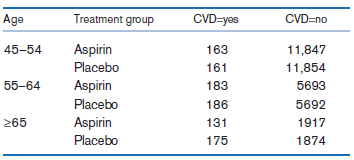
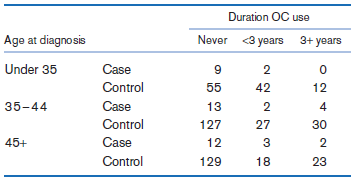
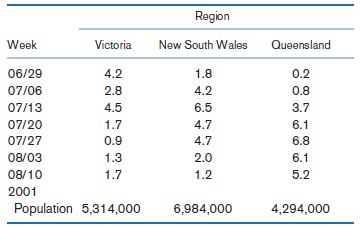
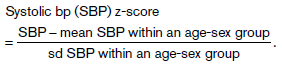Fundamentals Of Biostatistics 8th Edition Bernard Rosner - Solutions
Discover the comprehensive answers key and solution manual for "Fundamentals of Biostatistics 8th Edition" by Bernard Rosner. Access detailed solutions PDF and solved problems that offer step-by-step answers to enhance your understanding of biostatistics. Our extensive collection includes questions and answers, chapter solutions, and a test bank tailored for students and instructors alike. Whether you're seeking an instructor manual or a textbook supplement, our resources provide the guidance you need. Enjoy the convenience of a free download, ensuring you have the essential tools to excel in your studies with ease.
Get 50% OFF
Claim Now
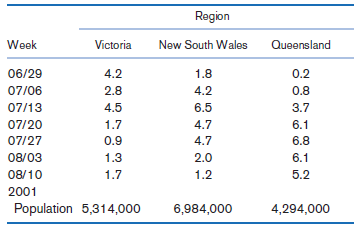
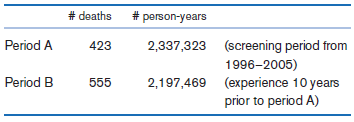
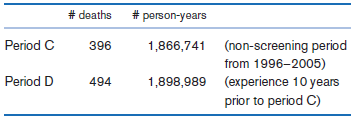
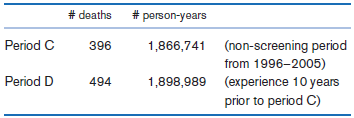
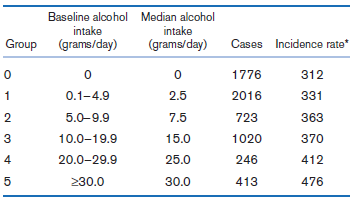
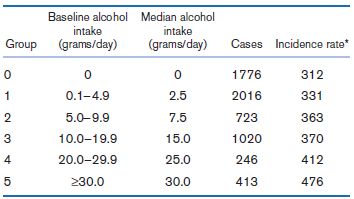
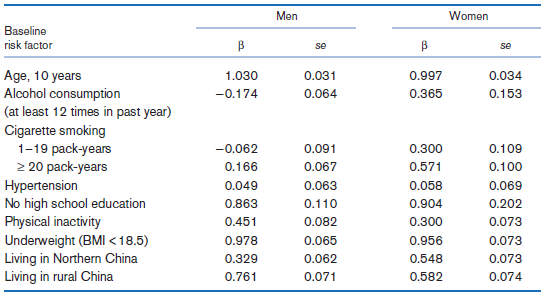
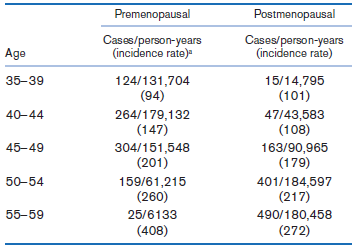
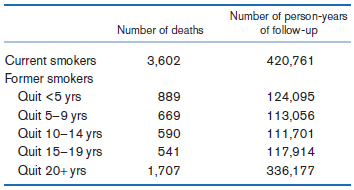
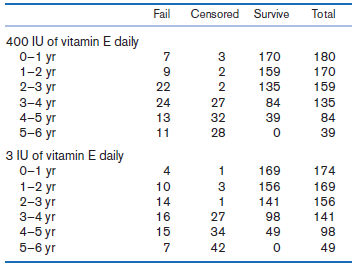
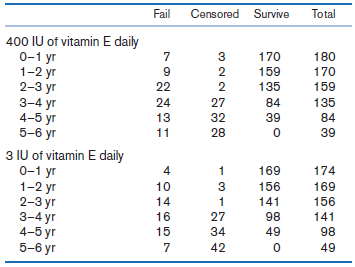
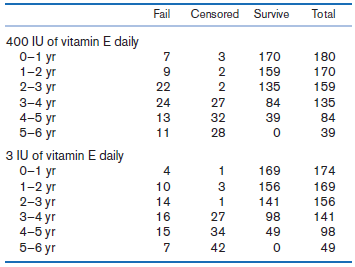
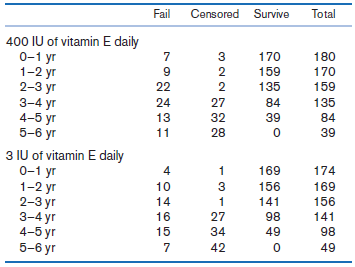
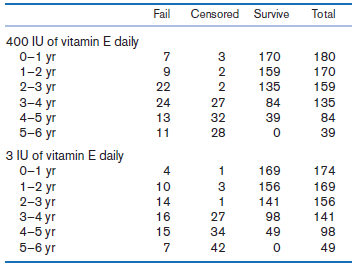
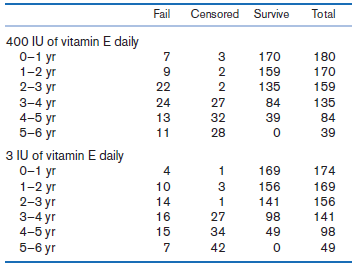
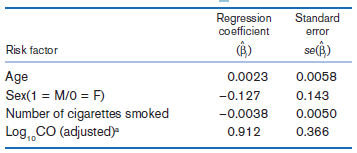
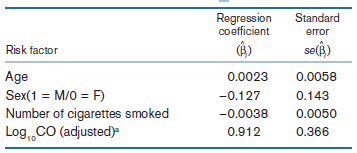
![logit case ageatmenarche race [fweight=freq] Logistic regression Number of obs 1907 LR chi2 (2) 15.76 Prob style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1526/5/5/6/4535afd67254be2b1526556437369.jpg)
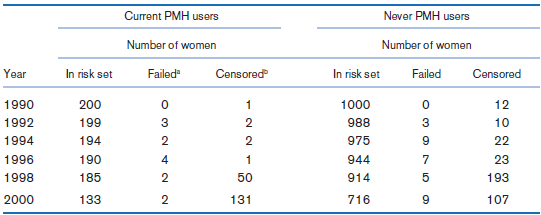
![logit case ageatmenarche race agemenarche_race [fweight=freq] Logistic regression Number of obs 1907 LR chi2 (3) 18.66 P](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1526/5/5/6/5325afd6774d1a891526556523502.jpg)
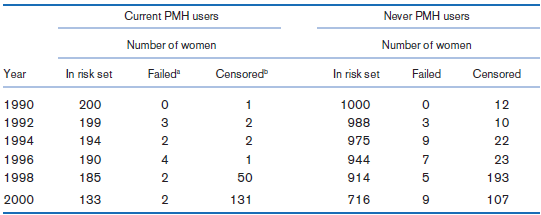
![logit case ageatmenarche race [fweight=freq] Logistic regression Number of obs 1907 LR chi2 (2) 15.76 Prob style=](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1526/5/5/6/6125afd67c4ec6b81526556600382.jpg)
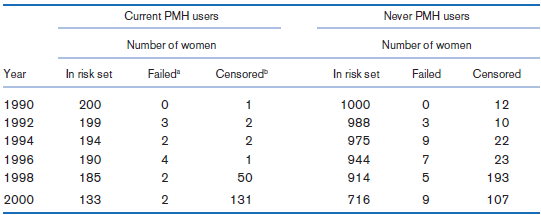
![logit case ageatmenarche race agemenarche_race [fweight=freq] Logistic regression Number of obs 1907 LR chi2 (3) 18.66 P](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1526/5/5/6/6135afd67c5501a51526556600763.jpg)
