In Exercises, we show that, as the number of subintervals increases indefinitely, the Riemann sum approximation of the area under the graph of f(x) = x² from 0 to 1 approaches the value 1/3, which is the exact value of the area.

Partition the interval [0, 1] into n equal subintervals of length Δx = 1/n each, and let x₁, x₂,......, x_n denote the right endpoints of the subintervals. Let

denote the Riemann sum that estimates the area under the graph of f (x) = x² on the interval 0 ≤ x ≤ 1.

(a) Show that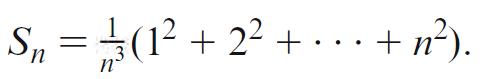

(b) Using the previous exercise, conclude that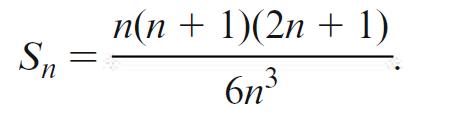

(c) As n increases indefinitely, S_n approaches the area under the curve. Show that this area is 1/3.

Sn [f(x) + f(x)+ + f(xn)]Ax =