Develop an M-file function to implement adaptive quadrature based on Fig. 20.6. Test the function by using it to determine the integral of the polynomial from Example 20.1. Then use it to solve Prob. 20.20.

Fig.20.6

Example 20.1

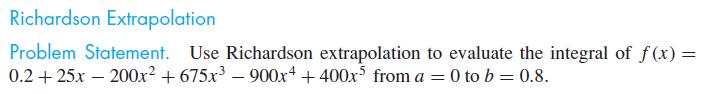
Problem 20.20

The upward velocity of a rocket can be computed by  the following formula:

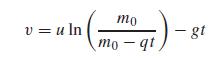
where ν = upward velocity, u = velocity at which fuel is expelled relative to the rocket, m₀ = initial mass of the rocket at time t = 0, q = fuel consumption rate, and g = downward acceleration of gravity (assumed constant = 9.81 m/s²). If u = 1850 m/s, m₀ = 160,000 kg, and q = 2500 kg/s, determine how high the rocket will fly in 30 s.

function q = quadadapt (f, a, b, tol, varargin) * Evaluates definite integral of f(x) from a to b if nargin < 4 | isempty (tol), tol c = (a + b)/2; 1. e-6; end fa = feval (f, a, varargin{:}); feval (f, c, varargin{:}); fc = fb = feval (f, b, varargin{:}); quadstep (f, a, b, tol, fa, fc, fb, varargin{:}); q = end function q = quadstep (f, a, b, tol, fa, fc, fb, varargin) Recursive subfunction used by quadadapt. h = b = a; c = (a + b)/2; fd = feval (f, (a+c)/2, varargin{:}); fe = feval (f, (c+b)/2, varargin{:}); q1h/6* (fa + 4*fc + fb); q2 = h/12 * (fa + 4*fd + 2*fc + 4*fe + fb); q1)