Perform the same calculation as in Prob. 24.22, but for the case where the tube is also insulated (i.e., no convection) and the right-hand wall is held at a fixed boundary temperature of 200 K.

Data From Problem 24.22

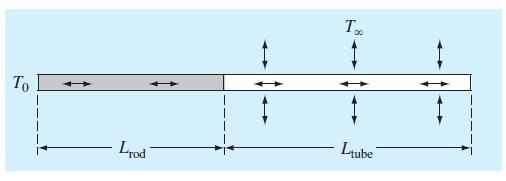
As in Fig. P24.22, an insulated metal rod has a fixed temperature (T₀) boundary condition at its left end. On it right end, it is joined to a thin-walled tube filled with water through which heat is conducted. The tube is insulated at its right end and convects heat with the surrounding fixed temperature air (T_∞). The convective heat flux at a location x along the tube (W/m2) is represented by J_conv = h(T_∞ − T₂(x)) where h = the convection heat transfer coefficient [W/(m² · K)]. Employ the finite-difference method with Δx = 0.1 m to compute the temperature distribution for the case where both the rod and tube are cylindrical with the same radius r (m). Use the following parameters for your analysis: L_rod = 0.6 m, L_tube = 0.8 m, T₀ = 400 K, T_∞ = 300 K, r = 3 cm, ρ₁ = 7870 kg/m³, Cp₁ = 447 J/(kg · K), k₁ = 80.2 W/(m · K), ρ₂ = 1000 kg/m³, Cp₂ = 4.18 kJ/(kg . K), k₂ = 0.615 W/(m · K), and h = 3000 W/(m² . K). The subscripts designate the rod (1) and the tube (2).

To Lrod Too Ltube