An article in Quality Engineering [A Comparison of Multi-Response Optimization: Sensitivity to Parameter Selection (1999, Vol. 11,

An article in Quality Engineering [€œA Comparison of Multi-Response Optimization: Sensitivity to Parameter Selection€ (1999, Vol. 11, pp. 405€“415)] conducted a half replicate of a 2⁵factorial design to optimize the retort process of beef stew MREs, a military ration. The design factors are x₁= sauce viscosity, x₂= residual gas, x₃= solid/liquid ratio, x₄= net weight, x₅= rotation speed. The response variable is the heating rate index, a measure of heat penetration, and there are two replicates.

(a) Estimate the factor effects. Based on a normal probability plot of the effect estimates, identify a model for the data from this experiment.

(b) Conduct an ANOVA based on the model identified in part

(a). What are your conclusions?

(c) Analyze the residuals and comment on model adequacy.

(d) Find a regression model to predict yield in terms of the coded factor levels.

(e) This experiment was replicated, so an ANOVA could have been conducted without using a normal plot of the effects to tentatively identify a model. What model would be appropriate? Use the ANOVA to analyze this model and compare the results with those obtained from the normal probability plot approach.

Transcribed Image Text:

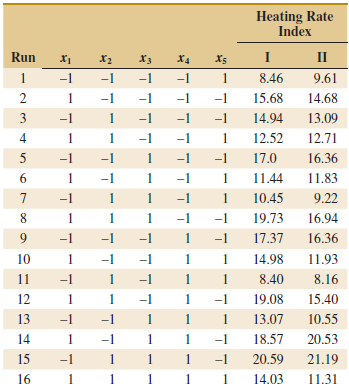
Heating Rate Index Run II x2 X3 X4 X5 -1 -1 1. -1 8.46 9.61 -1 -1 2 1 15.68 14.68 13.09 3 -1 1 -1 -1 14.94 12.52 12.71 4 1 1 -1 -1 1 -1 -1 -1 17.0 16.36 6. -1 -1 11.44 11.83 -1 1 1 1 10.45 9.22 8. 1 1 -1 -1 19.73 16.94 16.36 -1 1 -1 17.37 -1 10 -1 1 14.98 11.93 11 -1 1 -1 1 8.40 8.16 12 1 1 -1 1 -1 19.08 15.40 13 -1 1 1 13.07 10.55 -1 14 1 -1 1 -1 18.57 20.53 15 -1 1 1 1 -1 20.59 21.19 16 1 1 1 1 14.03 11.31