In this question, we consider the efficiency of variable elimination as a function of the elimination ordering. For any variable, X, let |X| denote the size of X’s range (the number of values it can take). At any stage in the variable elimination process, there will be a set of factors F = {F₁, . . . F_n}. Each factor Fi can be written as P(L_i | R_i), where Li and R_i are both sets of variables (for simplicity, assume that there is no evidence). For any variable X, we define I(X) to be the set of indices of factors that include X: I(X) = {i | X ∈ (L_i∪R_i)}.

When eliminating a specific variable, Y , we start by joining the appropriate factors from F to create a single joined factor, called join(Y, F). Note that join(Y, F) is created before performing the elimination step, so it still includes Y. 

a. For a given factor, F, we use size(F) to denote the size of the table needed to represent F. Give a precise general expression for size(join(Y, F)), using the notation above. 

b. Consider a generic Bayes net with variables X ∈ V that encodes a set of initial factors F0, where the query is to compute the marginal P(Q). Formulate a standard search problem (as in Chapter 3) that determines the optimal variable elimination ordering, where cost is measured by the sum of the sizes of the tables created during elimination. Note that for this problem we are only concerned with the sum of the sizes of the tables created by the join step, not the smaller tables that are subsequently created by the eliminate step. (You may also find it helpful to use the notation eliminate(X, F) to denote the result of summing over values of a variable X to eliminate X from factor F.) 

c. Let W be the set of variables remaining to be eliminated and let parents(X) and children(X) denote the sets containing all of X’s parents/children in the Bayes net. Which of the following are admissible heuristics for the search problem you defined in part (b)? 

(i) |W| 

(ii) |F| 

(iii) Σ_X∈W|X| 

(iv) Π_X∈W |X| 

(v) Σ_X∈W (|X|Π _{Y∈parents(X)}|Y|)

(vi) Σ_X∈W (|X|Π_{Y∈children(X)}|Y|) 

d. Consider the query P(D | + e, +c) on the Bayes net given in Figure S13.39. Draw the complete search tree for finding the optimal elimination order for this problem. Annotate nodes with states, and annotate costs and actions on the edges.

Figure S13.39

Transcribed Image Text:

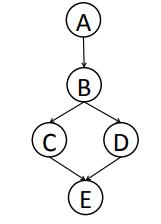
C A B E D