Question: Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides in choosing an appropriate model.

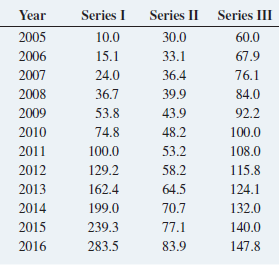
Series I Year Series II Series III 30.0 2005 10.0 60.0 2006 15.1 33.1 67.9 24.0 36.4 2007 76.1 84.0 2008 36.7 39.9 2009


For this problem, use each of the time series presented in the table above and stored in TSModel1:

a. Determine the most appropriate model.

b. Compute the forecasting equation.

c. Forecast the value for 2017.

Series I Year Series II Series III 30.0 2005 10.0 60.0 2006 15.1 33.1 67.9 24.0 36.4 2007 76.1 84.0 2008 36.7 39.9 2009 53.8 43.9 92.2 48.2 2010 74.8 100.0 100.0 2011 53.2 108.0 2012 129.2 58.2 115.8 2013 64.5 162.4 124.1 70.7 2014 199.0 132.0 2015 77.1 239.3 140.0 283.5 2016 83.9 147.8

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a Time Series I For Time Series I second differences are the most stable with values staying near 4 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Basic Business Statistics Questions!

Q:

Use the second naive forecasting model presented in this chapter to answer parts (a) through (c) of Exercise 2. Use P = 0.2 in preparing the forecast. Which model do you think works the best? Explain...

Q:

Although the time series data in Table P-18 are old, they provide the basis for some interesting regression modeling. Using the data in Table P-18, attempt to relate personal savings to personal...

Q:

The linear trend forecasting equation for an annual time series containing 22 values (from 1989 to 2010) on total revenues (in millions of dollars) is a. Interpret the Y intercept, b. Interpret the...

Q:

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides...

Q:

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides...

Q:

16.21 Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as...

Q:

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides...

Q:

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides...

Q:

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides...

Q:

Although you should not expect a perfectly fitting model for any time-series data, you can consider the first differences, second differences, and percentage differences for a given series as guides...

Q:

To rent a certain meeting room, a college charges a reservation fee $39 of and an additional fee $7.30 of per hour. The film club wants to spend at most $68.20 on renting the meeting room. What are...

Q:

A stock had the following trades during a particular period. What was the money flow for the stock? Is the money flow a positive or negative signal in this case? Price Volume $61.85 61.81 .............

Q:

Lincoln Park Company has a bond outstanding with a coupon rate of 5 . 6 2 percent and semiannual payments. The yield to maturity is 7 percent and the bond matures in 1 4 years. What is the market...

Q:

explain the meaning of the term shadow prices.

Q:

The following is the quadratic regression equation for a sample of n = 25: a. Predict Y for b. Suppose that the computed tSTAT test statistic for the quadratic regression coefficient is 2.35. At the...

Q:

Using the data of Problem 15.4 on page 637, stored in Domesticbeer, perform a square-root transformation on each of the independent variables (percentage alcohol and number of carbohydrates). Using...

Q:

Using the data of Problem 15.4 on page 637, stored in DomesticBeer, perform a natural logarithmic transformation of the dependent variable (calories). Using the transformed dependent variable and the...

Q:

The stock of the Belta Corporation has a beta of 1.1. The stock recently paid an annual dividend of $0.42, and dividends are expected to grow at a rate of 4% indefinitely. The equity premium has...

Q:

One measure of the health of a national economy is how quickly it creates jobs. One aspect of this issue is the number of jobs individual hold. As part of a study on job tenure, a survey was...

Q:

Assume the following information about projected cost and charges for a hospital in 2016: Fixed Costs = $10,000,000 Variable Cost per Inpatient Day = $200 Charge per Inpatient Day = $1,000. Initial...