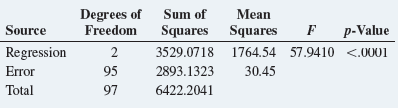
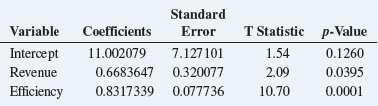
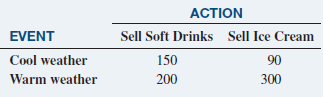
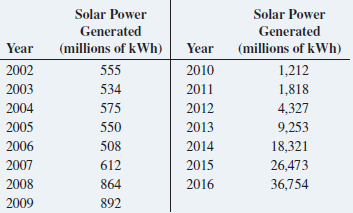
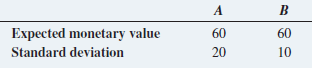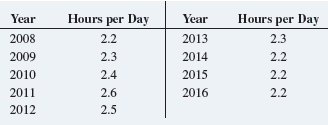Basic Business Statistics Concepts And Applications 14th Edition Mark L. Berenson, David M. Levine, Kathryn A. Szabat, David F. Stephan - Solutions
Discover comprehensive resources for "Basic Business Statistics Concepts And Applications 14th Edition" by Mark L. Berenson and others. Access the complete answers key and solutions manual online, offering step-by-step answers to solved problems and questions and answers from each chapter. Enhance your understanding with the instructor manual and test bank, ensuring thorough preparation. Whether you seek solutions in PDF format or need chapter solutions, our textbook answers provide a reliable guide. Enjoy the convenience of a free download, making it easier to grasp essential statistical concepts with ease.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()