In Example 2, change 2cos² x to 2sin² x.

Data from Example 2

Solve the equation 2 cos² x − sin x − 1 = 0 (0 ≤ x By use of the identity sin² x + cos² x = 1, this equation may be put in terms of sin x only. Thus, we have

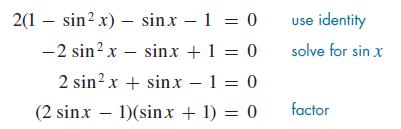
Setting each factor equal to zero, we find sin x = 1 2, or sin x = −1. For the domain 0 to 2π, sin x = 1/2 gives x = π/6, 5π/6, and sin x = −1 gives x = 3π/2. Therefore,

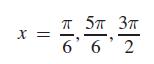
These values check when substituted in the original equation.

2(1 sin? x) sinx 1 = 0 2 sin2 x sinx +1 = 0 2 sin2 x + sinx 1=0 (2 sinx 1)(sinx +1) = 0 use identity solve for sin x factor