In Example 3, change −9y² to −y² and then follow the same instructions as in Exercise 1.

Data from Example 3

Determine the coordinates of the vertices and foci of the hyperbola 4x² − 9y² = 36 First, by dividing through by 36, we have

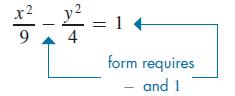
From this form, we see that a2 = 9 and b2 = 4. In turn, this tells us that a = 3, b = 2, and

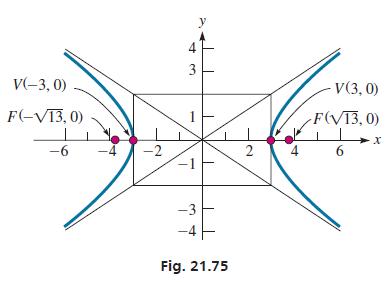
Because a² appears under x², the equation fits the form of Eq. (21.20). Therefore, the vertices are (−3, 0) and (3, 0) and the foci are (− 13, 0) and ( 13,0). The hyperbola is shown in Fig. 21.75.

9 y 4 = 1 || form requires - and 1