Make the given changes in the indicated examples of this section and then factor.

In Example 1, change the 3 to 4 and the 2 to 3.

Data from Example 1

In factoring x² + 3x + 2, we set it up as

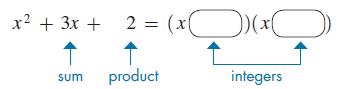
The constant 2 tells us that the product of the required integers is 2. Thus, the only possibilities are 2 and 1 (or 1 and 2). The + sign before the 2 indicates that the sign before the 1 and 2 in the factors must be the same. The + sign before the 3, the sum of the integers, tells us that both signs are positive. Therefore,

x² + 3x + 2 = (x + 2)(x + 1)

In factoring x² − 3x + 2, the analysis is the same until we note that the middle term is negative. This tells us that both signs are negative in this case. Therefore, 

x² − 3x + 2 = (x − 2)(x − 1)

For a trinomial with first term x 2 and constant +2 to be factorable, the middle term must be +3x or −3x. No other middle terms are possible. This means, for example, the expressions x² + 4x + 2 and x² − x + 2 cannot be factored.

x + 3x + 2 = (x( sum product ))(x) integers