Make the given changes in the indicated examples of this section and then solve the resulting problems.

In Example 1, change the + to − in the second equation and then solve the system of equations.

Data from Example 1

Solve the following system of equations by substitution

x − 3y = 6

2x + 3y = 3

Here, it is easiest to solve the first equation for x:

2(3y + 6) + 3y = 3

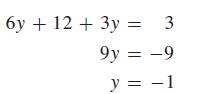
Now, put the value y = −1 into Eq. (A1) since this is already solved for x in terms of y. Solving for x, we have

x = 3(−1) + 6 = 3

Therefore, the solution of the system is x = 3, y = −1. As a check, substitute these values into each of the original equations. This gives us 3 − 3(−1) = 6 and 2(3) + 3(−1) = 3, which verifies the solution.

+ 12 + 3 = 3 9y=-9 y = -1