14. A randomvariable T is said to have a Weibull distribution with shape parameter > 0 and scale parameter > 0 if its

14. A randomvariable T is said to have a Weibull distribution with shape parameter α > 0 and scale parameter

β > 0 if its PDF is zero for t

The CDF of aWeibull(α, β) distribution has the following closed form expression:

When α = 1 the Weibull PDF reduces to the exponential PDF with λ = 1/β. The mean and variance of a Weibull(α, β) distribution are given by

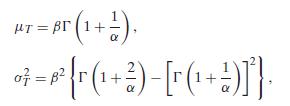
where - is the gamma function defined in Exercise 13.

(a) Use the R commands curve(dweibull(x, 0.5, 1), 0, 4), curve(dweibull(x, 1, 1), 0, 4, add=T, col=”red”), curve(dweibull(x, 1.5, 1), 0, 4, add=T, col=”blue”), and curve(dweibull(x, 2, 1), 0, 4, add=T, col=”green”) to superimpose four Weibull PDFs, noting that the second corresponds to the exponential(1) distribution.

(b) One of the imbedded functions in R is the gamma function. Use the R commands 10*gamma(1+1/0.2)
and 10**2*(gamma(1+2/0.2)-gamma(1+1/0.2)**2) to find the mean and variance, respectively, of the Weibull(0.2, 10) distribution.

(c) Use the formula for the Weibull CDF given above to find P(20 ≤ T

(d) Find the 95th percentile of T having the Weibull(0.2, 10) distribution by solving the equation FT(t0.05) = 0.95, where FT is the Weibull CDF given above with parameters α = 0.2 and β = 10. Confirm your answer with the R command qweibull(0.95, 0.2, 10).

ft(t)=-1-(1/8) for t0. Ba