13. A random variable T has a gamma distribution with shape parameter > 0 and scale parameter > 0 if its PDF is

13. A random variable T has a gamma distribution with shape parameter α > 0 and scale parameter β > 0 if its PDF is zero for negative values and

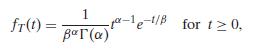
where - is the gamma function defined by -(α) = ∞0 tα−1e−tdt. The most useful properties of the gamma function are: -(1/2) = π1/2, -(α) = (α − 1)-(α − 1), for α >1, and -(r) = (r − 1)! for an integer r ≥ 1.
The mean and variance of a gamma(α, β) distribution are given by

When α = 1 we get the family of exponential distributions with λ = 1/β. Additionally, for α = r, with r integer ≥ 1, we get the family of Erlang distributions, which models the time until the rth occurrence in a Poisson process. Finally, the chi-square distribution with ν degrees of freedom, where ν ≥ 1 is an integer, denoted by χ2 ν , corresponds to α = ν/2 and β = 2.

(a) Use the R commands curve(dgamma(x, 1, 1), 0, 7, ylab=”Gamma PDFs”), curve(dgamma(x, 2, 1), 0, 7, add=T, col=2), and curve(dgamma(x, 4, 1), 0, 7, add=T, col=3) to superimpose the plots of three gamma PDFs corresponding to different parameter values. Superimpose the plots of the corresponding three gamma CDFs by making appropriate changes to these commands (dgamma changes to pgamma, and PDFs changes to CDFs).

(b) Using the formulas given above, compute the mean and variance of the gamma(2, 1), gamma(2, 2), gamma(3, 1), and gamma(3, 2) distributions.

(c) Use the R command qgamma(0.95, 2, 1) to find the 95th percentile of the gamma(2, 1) distribution.
Making appropriate changes to this command, find the 95th percentile of the gamma(2, 2), gamma(3, 1), and gamma(3, 2) distributions.

1 fr(t)= = Bar (a) 1-1 e -1-1/8 for t0,