A child is given an intelligence test. We assume that the test result x is N(, 100) where is the true intelligence quotient of

A child is given an intelligence test. We assume that the test result x is N(θ, 100) where θ is the true intelligence quotient of the child, as measured by the test (in other words, if the child took a large number of similar tests, the average score would be θ). Assume also that, in the population as a whole,θ is distributed according to an N(100, 225) distribution. If it is desired, on the basis of the intelligence quotient, to decide whether to put the child into a slow, average or fast group for reading, the actions available arc:

a₁ : Put in slow group, that is, decide θ ∈ Θ₁ = (0, 90)

a₁ : Put in average group. that is, decide θ ∈ Θ₂ = [90, 100]

a₁ : Put in fast group, that is, decide θ ∈ Θ₃ = ( 100,∞).

A loss function ℒ (θ, a) of the following form might be deemed appropriate:

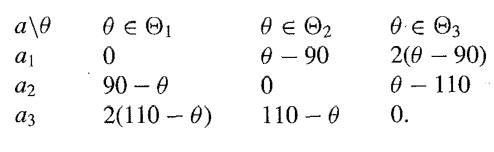
Assume that you observe that the test result x = 115. By using tables of the normal distribution and the fact that if ϕ p(t) is the density function of the standard normal distribution, then ∫ t ϕ (t) dt = -ϕ (t), find is the appropriate action to take on the basis of this observation.

a1 a2 (3 0 90 - 0 2(110 - 0) 0 - 90 0 110 - 0 2(0 - 90) 0-110 0.