In Example 6.3, estimate an MA(1) model in the differences \(z_{t}\) of the wholesale prices index using both methods applied in that example.

Data from Example 6.3

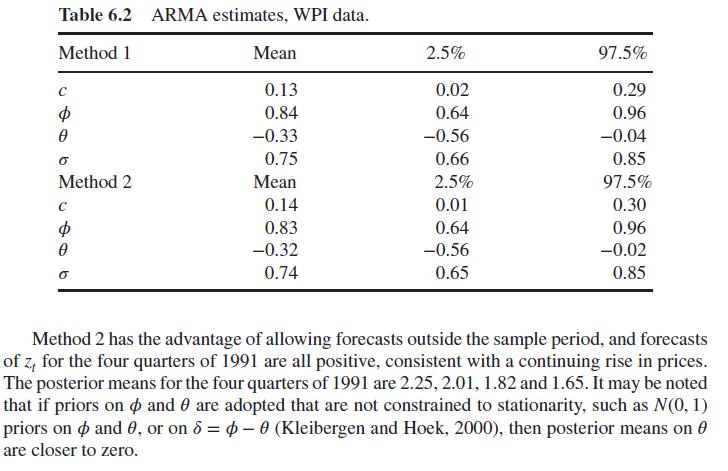
Consider data from Enders (2004, p. 87) on the US Wholesale Price Index (WPI), specifically quarterly data from 1960Q1, with y = 30.7, through to 1990Q4, with y224 = 116.2. Consider an ARMA(1, 1) model in the first differences Z = y+1 yr. The model may be written u~ N(0,). The errors at may be represented recursively as u-c-0-1- Ou-1 uc zo - Ouo. starting with To set the recursion going, one may generate latent pre-series values {zo, uo} using a dif- fuse prior on zo and assuming u N(0, 2). The log likelihood values for quarter t are then ~ log(L) = -0.5 log(2o) - 0.5u/(20), and one may use the dloglik option in OpenBUGS. Alternatively (method 2) one may represent the lagged residual as u-1=-1-Mt-1 (e.g. Marriott et al., 1996) so that Z~N(c+2-1+0 (z1-1 - M-1), 0). Zt Flat priors are adopted on c and zo, a uniform prior on , and priors on and are constrained to stationarity and invertibility. The second halves of two chain runs of 10000 iterations provide estimates (95% CRI) for c, d, and as in Table 6.2.