Let x 1 , x 2 , ... be a sequential sample from a Poisson distribution P(). Suppose that the stopping rule is to stop

Let x₁, x₂ , ... be a sequential sample from a Poisson distribution P(λ). Suppose that the stopping rule is to stop sampling at time n ≽ 2 with probability

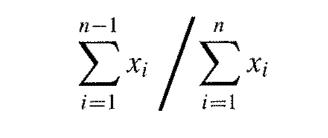
for n 2, 3, ... (define 0/0 = 1). Suppose that the first five observations are 3, 1, 2, 5, 7 and that sampling then stops. Find the likelihood function for A (Berger, 1985).

Xi Xi