With the data in the example in Section 3.4 on 'The Poisson distribution', would it be appropriate to reject the hypothesis that the true mean equalled the prior mean (i.e. that λ = 3)? [Use Lindley's method.]

The Poisson distribution

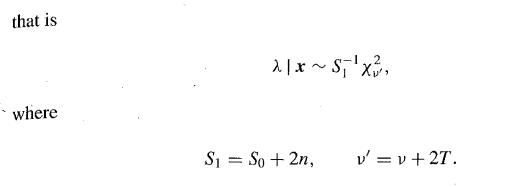
3.4.1 Conjugate prior A discrete random variable x is said to have a Poisson distribution of mean > if it has the density p(x2)= = 2* x! where T is the sufficient statistic exp(-2). This distribution often occurs as a limiting case of the binomial distribution as the index n and the parameter 0 but their product n (see Exercise 6 in Chapter 1). It is thus a useful model for rare events, such as the number of radioactive decays in a fixed time interval, when we can split the interval into an arbitrarily large number of sub-intervals in any of which a particle might decay, although the probability of a decay in any particular sub-interval is small (though constant). Suppose that you have n observations x = (x, x2,...,xn) from such a distribu- tion, so that the likelihood is 1(x) x exp(-n),