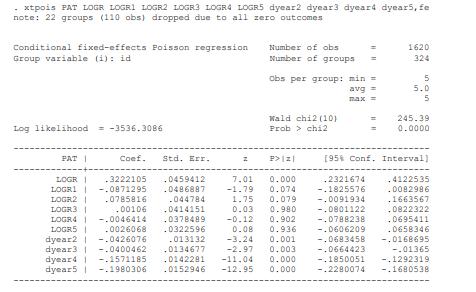
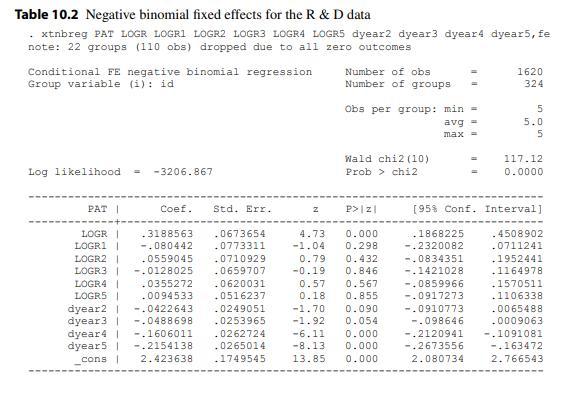
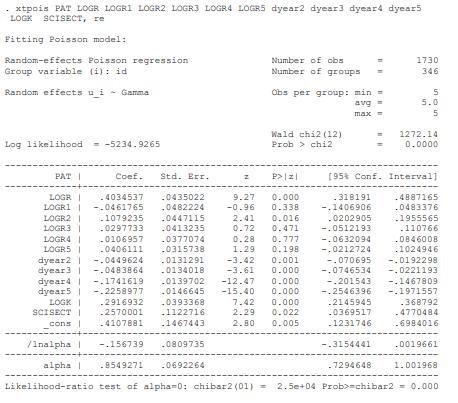
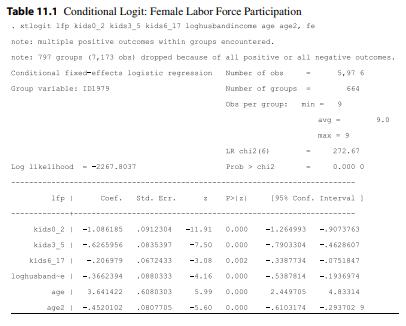
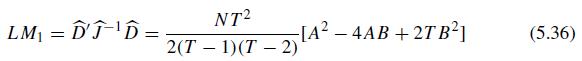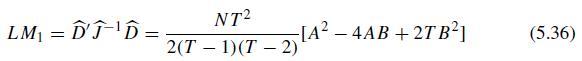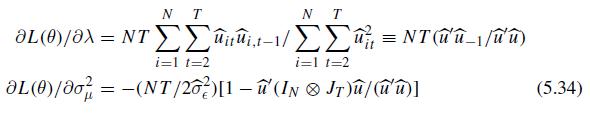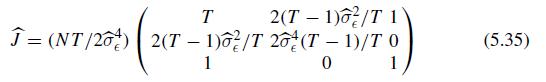Econometric Analysis Of Panel Data 6th Edition Badi H Baltagi - Solutions

Discover a comprehensive collection of questions and detailed answers from the "Econometric Analysis Of Panel Data 6th Edition" by Badi H Baltagi. Our platform offers an online solution manual, complete with step-by-step answers for each chapter. Access the answers key and solutions PDF to enhance your understanding of econometrics. With solved problems and an instructor manual, students and educators can explore the textbook's concepts thoroughly. Our test bank provides valuable questions and answers to test your knowledge and prepare for exams. Enjoy free downloads of chapter solutions, offering a convenient and accessible way to excel in your studies.