Exercise 13.13 Consider the SDE where (x) > 0, and let Y (t) = f(X(t)) for a sufficiently smooth function f(x). Suppose Prove

Exercise 13.13 Consider the SDE

where σ(x) ≥ ε > 0, and let Y (t) = f(X(t)) for a sufficiently smooth function f(x). Suppose

Prove that the function f(x) must be of the form

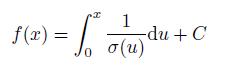
for some constant C. On the other hand, let Z(t) = g(X(t)) for a sufficiently smooth function g(x), and suppose

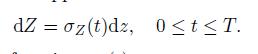
Determine the diffusion function σZ(t).

dX (X)dt+o(X)dz, 0