After adding the indicator variables for Colour, which showed different intercepts for the three different colour levels, an analyst wonders if the slopes for the three colour levels might be different as well, so she adds two more predictors, ColourD*Carat Weight and Colour \(G^{*}\) Carat Weight, to the model (see For Example: "Indicator variables for diamond colour"). The regression output shows:
Response Variable: \(\log _{10}\) Price
\(R^{2}=85.77 \%\) Adjusted \(R^{2}=85.67 \%\)
\(s=0.1085\) with \(749-6=743\) degrees of freedom

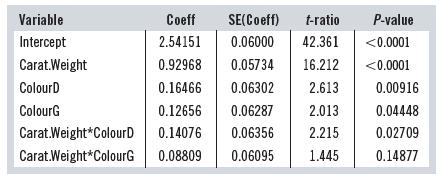
QUESTION:

Based on this, what model might you use to predict Log10 Price? What other factors should be taken into account?

Variable Coeff SE(Coeff) t-ratio P-value Intercept 2.54151 0.06000 42.361