Prove the second case of Theorem 3.6.

Data from in Theorem 3.6

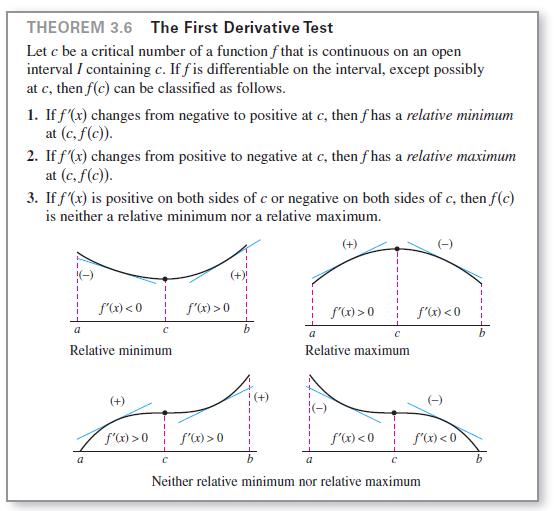
THEOREM 3.6 The First Derivative Test Let c be a critical number of a function f that is continuous on an open interval I containing c. If f is differentiable on the interval, except possibly at c, then f(c) can be classified as follows. 1. If f'(x) changes from negative to positive at c, then f has a relative minimum at (c, f(c)). 2. If f'(x) changes from positive to negative at c, then f has a relative maximum at (c, f(c)). 3. If f'(x) is positive on both sides of c or negative on both sides of c, then f(c) is neither a relative minimum nor a relative maximum. (+) a f'(x) < 0 Relative minimum a (+) f'(x) > 0 f'(x) > 0 f'(x) > 0 a f'(x) > 0 Relative maximum f'(x) < 0 f'(x)