Repeat Exercise 17 for the curve represented by the vector-valued function

Data from in Exercise 17

Consider the helix represented by the vector-valued function r(t) = (2 cos t, 2 sin t, t).

(a) Write the length of the arc s on the helix as a function of t by evaluating the integral

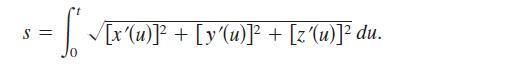
(b) Solve for t in the relationship derived in part (a), and substitute the result into the original set of parametric equations. This yields a parametrization of the curve in terms of the arc length parameter s.

(c) Find the coordinates of the point on the helix for arc lengths s = √5 and s = 4.

(d) Verify that

r(t) = (4(sin t t cos t), 4(cos t + t sin t), t).