Question: Show that the cubic polynomial p(x) = ax + bx + cx + d has exactly one point of inflection (x 0 , y 0

Show that the cubic polynomial p(x) = ax³ + bx² + cx + d has exactly one point of inflection (x0, y0), where

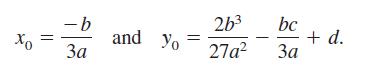
= -b and Yo = 263 27a bc + d.

Use this formula to find the point of inflection of p(x) = x³ - 3x² + 2.

= -b and Yo = 263 27a bc + d.

Step by Step Solution

★★★★★

3.38 Rating (164 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

px ax bx cx d px 3ax 2bx c px 6ax 2b 6ax 2b 0 The sign of px change... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Calculus 10th Edition Questions!

Q:

Show that the cubic spline basis functions {i}n+1i=0 are linearly independent.

Q:

Prove that a cubic function has exactly one point of inflection.

Q:

a. Show that the cubic polynomials P(x) = 3 2(x + 1) + 0(x + 1)(x) + (x + 1)(x)(x 1) And Q(x) = 1 + 4(x + 2) 3(x + 2)(x + 1) + (x + 2)(x + 1)(x) Both interpolate the data b. Why does part (a) not...

Q:

The scientific calculator is the most affordable and portable mathematics tool currently available among secondary and university students. One of the functions of the scientific calculator is the...

Q:

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Q:

Question 9 (1 point) At a point x = c where f'(c) = 0, f(c) is not guaranteed to be either a local maximum or minimum O True O FalseQuestion 10 (1 point) Which of the following functions has an...

Q:

math is connections Math Is Connections: A, B, C, D Project A cubic polynomial has four coefficients, A, B, C, D. S (x ) = Ax3 + BX? + CX + D Use your set of four integers from task 74 as A, B, C, D...

Q:

4:22 Page 6 of 8 Vista Virtual School - A3 7. The path of a baseball after it is hit is modelled by the equation h = -4.9812 + 10.751 +1.4, where h is the height, in metres, of the ball and t is the...

Q:

Programming Assignment 2: Find the zeros of a polynomial. Background: The zeros of a polynomial f(x) are the values of x for which f(x) = 0. In an interval (xlow, xhigh), a monotonic function f(x)...

Q:

1. For each of the following functions use the appropriate techniques to sketch a graph. Please show all of your work. A. f(x) = x - 8x + 7 [13] B. f (x) = 3x-1 x+1 [11] C. g(x) = X [16] x -4x+4 2....

Q:

How can the implementation of an accounting information system improve financial reporting accuracy and efficiency within a company? Provide at least three specific examples of how an AIS can...

Q:

Plz answer this as quickly as possible I've attached the formulas, it is due in less then 1hr30 I'll ???? if it's early 3. The confluent hypergeometric functions (A9.1), whose first parameter is a...

Q:

Read what Zara says. Show that she is right. 12 Read what Marcus says. Show that he is wrong. Explain the mistake Marcus has made. When I expand 5(2x+6)+2(3x-5), then collect like terms and finally...

Q:

Betty Cardinal runs Cardinals Book Shop in a downtown location. As her newly hired accountant, your task is to do the following (substituting HST at 13% for GST at 5% if your instructor so directs):...

Q:

The practice of charging interest on money that is lent by one party to another, while commonplace now, has been historically controversial. Major religions have prohibited the charging of interest...

Q:

Suppose the domestic demand and supply for corn intersects at p and suppose further that p also happens to be the world price for corn. (Since the domestic price is equal to the world price, there...

Q:

In our discussion of economic versus statutory incidence, the text has focused primarily on the incidence of taxes. This exercise explores analogous issues related to the incidence of benefits from...

Q:

Empire Electric Company (EEC) uses only debt and common equity. It can borrow unlimited amounts at an interest rate of rd=10% as long as it finances at its target capital structure, which calls for...

Q:

Using the data in exhibits C2.1 and C2.3, calculate and analyze the firms 2012 and 2013 ratios. Enter the ratios in the table below in the 2012 and 2013 columns, respectively: 2. Part of Owens...

Q:

a. (4 points) You purchased a zero coupon bond one year ago for \$249.95. The market interest rate is now 9 percent (please keep in mind that this number is compounded semi-annually by convention)....