Question: A uniform magnetic field (mathbf{B}) has constant strength (b) in the (z)-direction [i.e., (mathbf{B}=langle 0,0, bangle) ]. (a) Verify that (mathbf{A}=frac{1}{2} mathbf{B} times mathbf{r}) is
A uniform magnetic field \(\mathbf{B}\) has constant strength \(b\) in the \(z\)-direction [i.e., \(\mathbf{B}=\langle 0,0, bangle\) ].
(a) Verify that \(\mathbf{A}=\frac{1}{2} \mathbf{B} \times \mathbf{r}\) is a vector potential for \(\mathbf{B}\), where \(\mathbf{r}=\langle x, y, 0angle\).
(b) Calculate the flux of \(\mathbf{B}\) through the rectangle with vertices \(A, B, C\), and \(D\) in Figure 19.
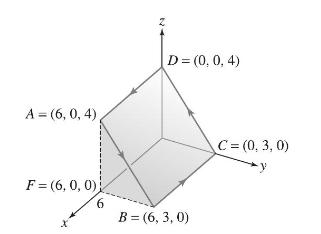
A = (6, 0, 4) F=(6, 0, 0); 6 D = (0, 0, 4) B = (6,3,0) C = (0,3,0) y
Step by Step Solution
3.35 Rating (155 Votes )
There are 3 Steps involved in it
a To verify that a given vector mathbfA is a vector potential for a magnetic field mathbfB we need to show that mathbfB is the curl of mathbfA that is ... View full answer

Get step-by-step solutions from verified subject matter experts


