The magnetic field \(\mathbf{B}\) due to a small current loop (which we place at the origin) is called a magnetic dipole (Figure 18). For \(ho\) large, \(\mathbf{B}=\operatorname{curl}(\mathbf{A})\), where

\[
\mathbf{A}=\left\langle-\frac{y}{ho^{3}}, \frac{x}{ho^{3}}, 0ightangle \text { and } ho=\sqrt{x^{2}+y^{2}+z^{2}}
\]

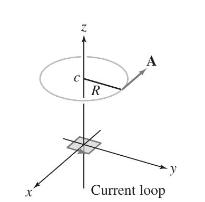
(a) Let \(C\) be a horizontal circle of radius \(R\) with center \((0,0, c)\), where \(c\) is large. Show that \(\mathbf{A}\) is tangent to \(C\).
(b) Use Stokes' Theorem to calculate the flux of \(\mathbf{B}\) through \(C\).

X Z R A Current loop