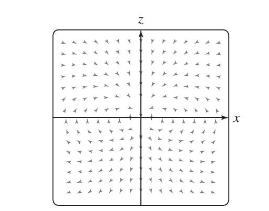
Question: The electric field due to a unit electric dipole oriented in the (mathbf{k})-direction is (mathbf{E}=ablaleft(z / r^{3}ight)), where (r=) (left(x^{2}+y^{2}+z^{2}ight)^{1 / 2}) (Figure 20). Let
The electric field due to a unit electric dipole oriented in the \(\mathbf{k}\)-direction is \(\mathbf{E}=abla\left(z / r^{3}ight)\), where \(r=\) \(\left(x^{2}+y^{2}+z^{2}ight)^{1 / 2}\) (Figure 20). Let \(\mathbf{e}_{r}=r^{-1}\langle x, y, zangle\).
(a) Show that \(\mathbf{E}=r^{-3} \mathbf{k}-3 z r^{-4} \mathbf{e}_{r}\).
(b) Calculate the flux of \(\mathbf{E}\) through a sphere centered at the origin.
(c) Calculate \(\operatorname{div}(\mathbf{E})\).
(d) Can we use the Divergence Theorem to compute the flux of \(\mathbf{E}\) through a sphere centered at the origin?
N K
Step by Step Solution
3.29 Rating (161 Votes )
There are 3 Steps involved in it
It looks like youre studying the electric field produced by a dipole To solve the problems youve presented well need to consider some concepts and formulas from electromagnetism and vector calculus Un... View full answer

Get step-by-step solutions from verified subject matter experts


