We define the first difference of a function by (x) = (x + 1) (x). Show that if then P

We define the first difference δ ƒ of a function ƒ by δ ƒ(x) = ƒ(x + 1) − ƒ(x).

Show that if

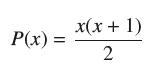
then δP = (x + 1). Then apply Exercise 46 to conclude that

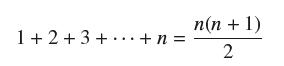
Data From Exercise 46

We define the first difference δ ƒ of a function ƒ by δ ƒ(x) = ƒ(x + 1) − ƒ(x).

Suppose we can find a function P such that δP(x) = (x + 1)^k and P(0) = 0. Prove that P(1) = 1^k , P(2) = 1^k + 2^k, and, more generally, for every whole number n,

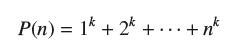
P(x)= x(x + 1) 2