Consider the sequence {F_n} defined by

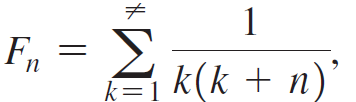
for n = 0, 1, 2, c. When n = 0, the series is a p-series, and we have F₀ = π²/6 (Exercises 65 and 66).

a. Explain why {F_n} is a decreasing sequence.

b. Plot {F_n}, for n = 1, 2, . . . , 20.

c. Based on your experiments, make a conjecture about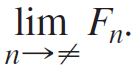

Data from Exercise 65

The Riemann zeta function is the subject of extensive research and is associated with several renowned unsolved problems. It is defined by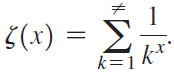When x is a real number, the zeta function becomes a p-series. For even positive integers p, the value of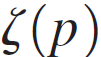is known exactly. For example,

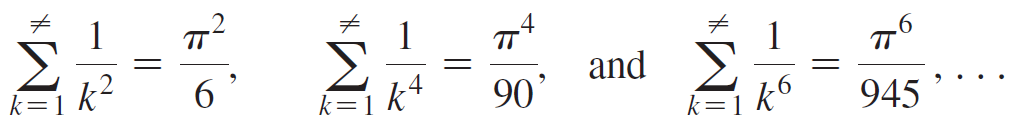
Use the estimation techniques described in the text to approximate 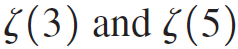(whose values are not known exactly) with a remainder less than 10^-3.

Data from Exercise 66

In 1734, Leonhard Euler informally proved that 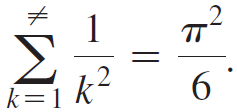An elegant proof is outlined here that uses the inequality

cot² x 2 2 x (provided that 0

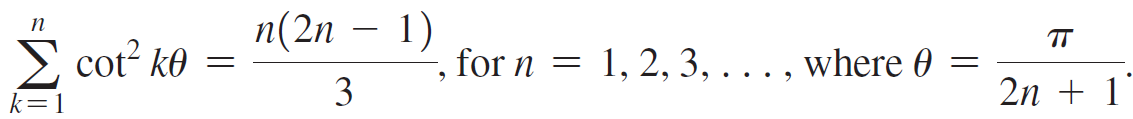
- k(k + n) k=1 lim Fp. >#