In 1734, Leonhard Euler informally proved that An elegant proof is outlined here that uses the inequality cot 2 x < 1/x 2 < 1

In 1734, Leonhard Euler informally proved that 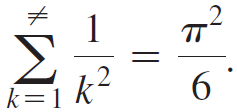An elegant proof is outlined here that uses the inequality

cot² x 2 2 x (provided that 0

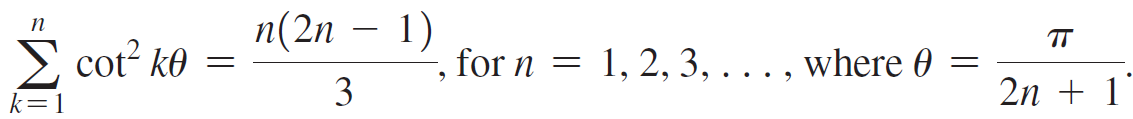
a. Show that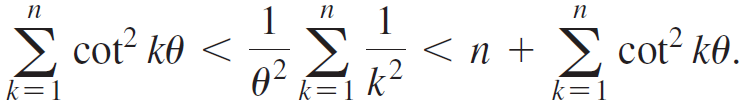

b. Use the inequality in part (a) to show that

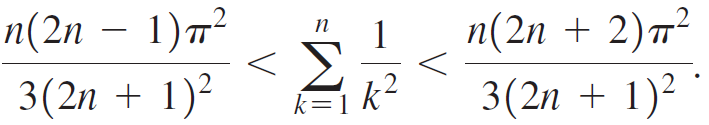
c. Use the Squeeze Theorem to conclude that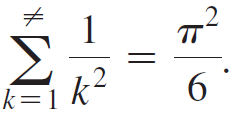

.2 TI 1 6 k2 k=1 n(2n 1) TT E cot? ko , for n = 1, 2, 3, . . . , where 0 3 2n + 1