Prove Theorem 4.2 for a local maximum: If f has a local maximum value at the point c and f'(c) exists, then f'(c) = 0. Use the following steps.

a. Suppose f has a local maximum at c. What is the sign of f(x) - f(c) if x is near c and x > c? What is the sign of f(x) - f(c) if x is near c and x < c?

b. If f'(c) exists, then it is defined by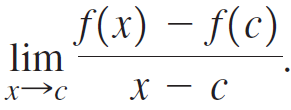Examine this limit as x → c⁺ and conclude that f'(c) ≤ 0.

c. Examine the limit in part (b) as x → c^- and conclude that f'(c) ≥ 0.

d. Combine parts (b) and (c) to conclude that f'(c) = 0.

f(x) f(c) lim