Question: We found the least squares line through a set of n points(x 1 , y 1 ), (x 2 , y 2 ) ,....,(x n
We found the least squares line through a set of n points(x1 , y1), (x2 , y2) ,....,(xn , yn) by choosing the slope of the line m and the y-intercept b to minimize the quantity S(m, b) = ∑(mx + b - y)2, where the summation symbol ∑ means that we sum over all the data points. Minimize S by setting Sm(m, b) = 0 and Sb(m, b) = 0, and then rearrange the results to derive the equations from Section 1.3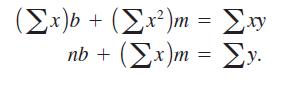
(x)b + (x)m nb + (x)m + = =
Step by Step Solution
3.34 Rating (163 Votes )
There are 3 Steps involved in it
If S m mb 0 then ... View full answer

Get step-by-step solutions from verified subject matter experts


