Question: A 2 J table has ordinal response. Let F j|i = 1|i + ..... + j|i . When F j|2 F

A 2 Ã— J table has ordinal response. Let F_j|i= Ï€_1|i+ ..... + Ï€_j|i. When F_j|2‰¤ F_j|1for j = 1,......, J, the conditional distribution in row 2 is stochastically higher than the one in row 1. Consider the cumulative odds ratios

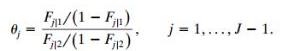
F1/(1 - F) Fj2/(1 - Fj2)

Show that log Î¸_j> 0 for all j is equivalent to row 2 being stochastically higher than row 1. Explain why row 2 is then more likely than row 1 to have observations at the high end of the ordinal scale.

F1/(1 - F) Fj2/(1 - Fj2)" j = 1..., J - 1.

Step by Step Solution

★★★★★

3.48 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

log j 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Categorical Data Analysis Questions!

An I Ã J table has ordered columns and unordered rows. Ridits (Bross 1958) are data-based column scores. The jth sample ridit is the average cumulative proportion within category j, The sample...

A five-year follow-up study was carried out in a certain metropolitan area to assess the relationship of diet and weight to the incidence of stomach cancer. Data were obtained on n = 2,000 subjects....

The following two-way table gives data for a 2 Ã 3 factorial experiment with two observations for each factor-level L09067 combination. a. Identify the treatments for this experiment....

Exercises Chapter 2 2.1 Marginal and conditional probability: The social mobility data from Section 2.5 gives a joint probability distribution on (Y1 , Y2 )= (father's occupation, son's occupation)....

Chapter 15, \"More Probability\" from Applied Finite Mathematics by Rupinder Sekhon was developed by OpenStax College, licensed by Rice University, and is available on the Connexions website. It is...

Q9some type is wrong, can refer to the attach file. In a study of the relationship between an explanatory variable Z and a response variable Y , n independent observations are taken in the form of...

Len and Christy Vole, ages 42 and 39 respectively, are married and file jointly in 2014. Len is a contractor operating as a sole proprietorship (EIN 11-1111111). Christy is employed, earning $24,000...

Name : BIST 512 : Categorical Data Analysis Final Exam May 9th, 2pm to 4:30pm There are seven problems. Read all problems carefully before starting. Put your name on every sheet of paper before you...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

How do I set up Excel to solve the Chase Bank Case Study? I am really struggling with how to set it up to make Solver work. Here is the case study. Total Cost: total cost of $3253.34 Chase Manhattan...

FiberCom, Inc., a manufacturer of fiber optic communications equipment, uses a job order costing system. Since the production process is heavily automated, manufacturing overhead is applied on the...

Chamberlane Ltd is an agricultural company quoted on the JSE. The directors of the company hold 52% of the issued share capital between them and have asked you to value the business. The Directors of...

Sewell Ent. Earned $ 1 5 0 million last year after taxes, and retained $ 9 0 million. Calculate the dividend payout ratio.

The greeting approach is used when a customer is examining a specific item for sale.

A teacher announces a pop quiz for which the student is completely unprepared. The quiz consists of 100 true-false questions. The student has no choice but to guess the answer randomly for all 100...

Answer true of false for each part. a. When you flip a coin ten times, you are more likely to get the sequence HHHHHTTTTT than the sequence HHHHHHHHHH. b. When you flip a coin ten times, you are more...

An eyewitness to the crime says that the person who committed it was male, between 15 and 20 years old, Hispanic, and drove a blue Honda. The prosecutor points out that a proportion of only 0.001...

Suppose you have saved $4,000 for a down payment on a new car. The largest monthly payment you can afford is $350. The loan will have a 24% APR based on end-of-month payments. Use a financial...

Using the data in the following table, , estimate the average return and volatility for each stock. The return of stock A is 2 . 3 3 % . ( Round to two decimal places. ) The return of stock B is 8 ....

Use the following information to find the weighted average cost of capital for Bellevue Power Co. Debt: 5,000 seven percent coupon bonds outstanding, $1,000 par value, 20 years to maturity, selling...