For a study using logistic regression to determine characteristics associated with remission in cancer patients, Table 5.10 shows the most important explanatory variable, a labeling index (U). This index measures proliferative activity of cells after a patient receives an injection of tritiated thymidine, representing the percentage of cells that are €œlabeled.€™ The response Y measured whether the patient achieved remission (1 = yes). Software reports Table 5.11 for a logistic regression model using LI to predict the probability of remission.

Table 5.10:

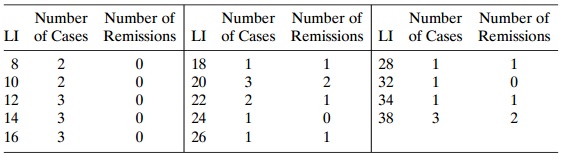
Table 5.11:

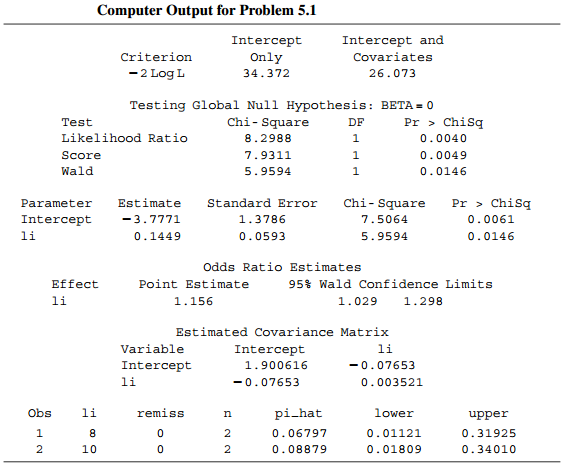
a. Show how software obtained π̂ = 0.068 when LI = 8.

b. Show that π̂ = 0.5 when LI = 26.0.

c. Show that the rate of change in π̂ is 0.009 when LI = 8 and 0.036 when LI = 26.

d. The lower quartile and upper quartile for LI are 14 and 28. Show that π̂ increases by 0.42, from 0.15 to 0.57, between those values.

e. For a unit change in LI, show that the estimated odds of remission multiply by 1.16. LEMS 199

f. Explain how to obtain the confidence interval reported for the odds ratio. Interpret.

g. Construct a Wald test for the effect. Interpret.

h. Conduct a likelihood-ratio test for the effect, showing how to construct the test statistic using the €“2 log L values reported.

Number Number of Number Number of LI of Cases Remissions LI of Cases Remissions LI of Cases Remissions Number Number of 28 32 34 38 18 20 2 10 2 3 12 3 2 24 26 22 14 3 3 3 16 Computer Output for Problem 5.1 Intercept and Covariates 26.073 Intercept Criterion Only -2 Log L 34.372 Testing Global Null Hypothesis: BETA = 0 Test Chi- Square DF Pr > Chisqg Likelihood Ratio 8.2988 0.0040 Score 7.9311 0.0049 Wald 5.9594 0.0146 Parameter Estimate Standard Error Chi- Square Pr > Chisg Intercept -3.7771 1.3786 7.5064 0.0061 li 0.1449 0.0593 5.9594 0.0146 Odds Ratio Estimates Effect Point Estimate 95% Wald Confidence Limits li 1.156 1.029 1.298 Estimated Covariance Matrix Variable Intercept li Intercept 1.900616 -0.07653 li -0.07653 0.003521 Obs li remiss pi_hat lower upper 0.06797 0.01121 0.31925 10 0.08879 0.01809 0.34010