Consider a vapor condensing on a wall and forming a liquid film. Assume that locally the film
Question:
Consider a vapor condensing on a wall and forming a liquid film. Assume that locally the film thickness is related to the flow rate per unit transfer area by momentum-transfer considerations.
Then show that the change in mass flow rate is related to the film thickness as per the following equation:
\[\frac{d \dot{m}}{d x}=\frac{ho^{2} g \delta^{2}}{\mu} \frac{d \delta}{d x}\]
From a heat balance show that the change in mass flow rate is given by
\[\hat{h}_{\lg } \frac{d \dot{m}}{d x}=\frac{k_{1}}{\delta}\left[T_{\mathrm{sat}}-T_{\mathrm{w}}\right]\]
Equate the two expressions for the change in \(\dot{m}\) and and derive an expression for \(d \delta / d x\). Integrate this expression and derive an expression for \(\delta\) as a function of \(x\). Verify that the resulting expression is the same as Eq. (18.62). Find an expression for the local heat transfer coefficient and verify that it is proportional to \(x^{-1 / 4}\).
Find an expression for the average heat transfer coefficient for a wall of height \(L\) by integration of the local value.
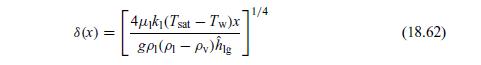
Step by Step Answer:

Advanced Transport Phenomena Analysis Modeling And Computations
ISBN: 9780521762618
1st Edition
Authors: P. A. Ramachandran





