The boundedness theorem shows how the bottom row of a synthetic division is used to place upper
Question:
The boundedness theorem shows how the bottom row of a synthetic division is used to place upper and lower bounds on possible real zeros of a polynomial function. Let P(x) define a polynomial function of degree n ≥ 1 with real coefficients and with a positive leading coefficient. If P(x) is divided synthetically by x - c and (a) if c > 0 and all numbers in the bottom row of the synthetic division are nonnegative, then P(x) has no zero greater than c; (b) if c
Use the boundedness theorem to show that the real zeros of each polynomial function satisfy the given conditions.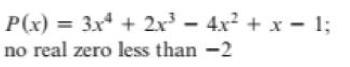
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

College Algebra With Modeling And Visualization
ISBN: 9780134418049
6th Edition
Authors: Gary Rockswold
Question Posted:





